Demonstration of DetectImports principle
Xavier Didelot
2024-01-31
Source:vignettes/principle.Rmd
principle.RmdSimulation with constant population size
For initial simplicity, consider that the local population has constant effective population size \(N_e\).
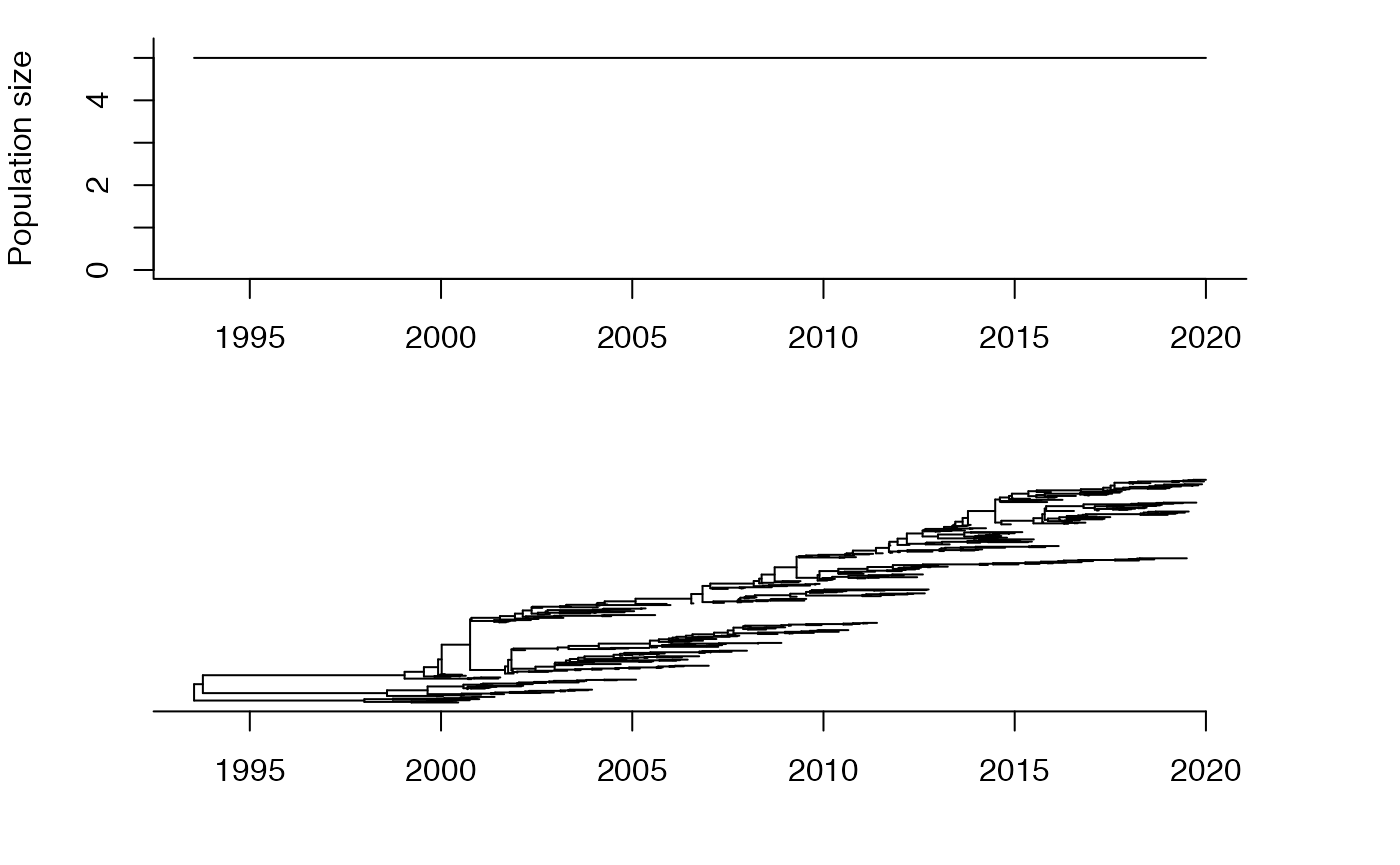
Coalescent intervals
We consider the leaves \(k=1..n\) in increasing order of date. Let \(s_k\) denote the date of leaf \(k\), we have \(i<j \implies s_i<s_j\). The \(k\)-th leaf has to coalesce with the genealogy formed by the \((k-1)\) first leaves. Let \(C_k\) denote the sum of branch lengths in the genealogy formed so far between the time of leaf \(k\) and the time where it coalesces with an ancestor of a previously considered leaf. We call \(A_i\) the ``coalescent interval’’. Let’s plot \(C_k\) on the y-axis against \(s_k\) on the x-axis:
plotCoalInt(tree)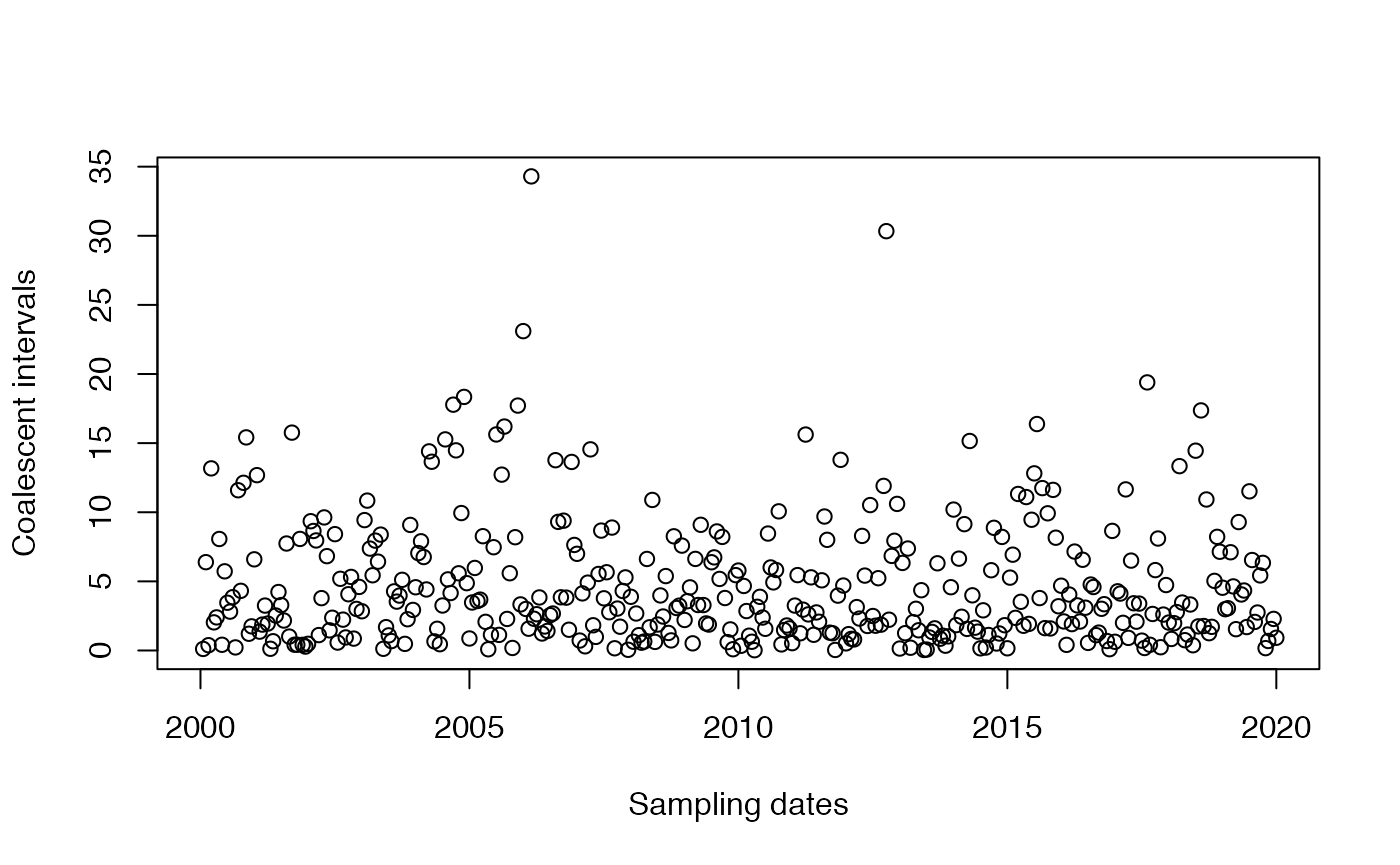
Detection of imports
Imports are likely to have \(C_k\) greater than expected if transmission happened only locally. In the case where the location population size is constant equal to \(N_e\), \(C_k\) is exponentially distributed with mean \(N_e\). So we can detect imports by looking for coalescent intervals that are greater than this. Since \(N_e\) is unknown, we need to estimate it from the data. A simple estimator would be to take the mean of the \(C_k\), but since we suspect that some \(C_k\) are affected by imports, it is preferable to use an estimator based on the median: \[\hat N_e=\frac{\mathrm{median}(C_{1..n})}{\mathrm{ln}(2)}\] Of course here there are no imports:
res=detectImportsFAST(tree,constant=T)
plot(res)
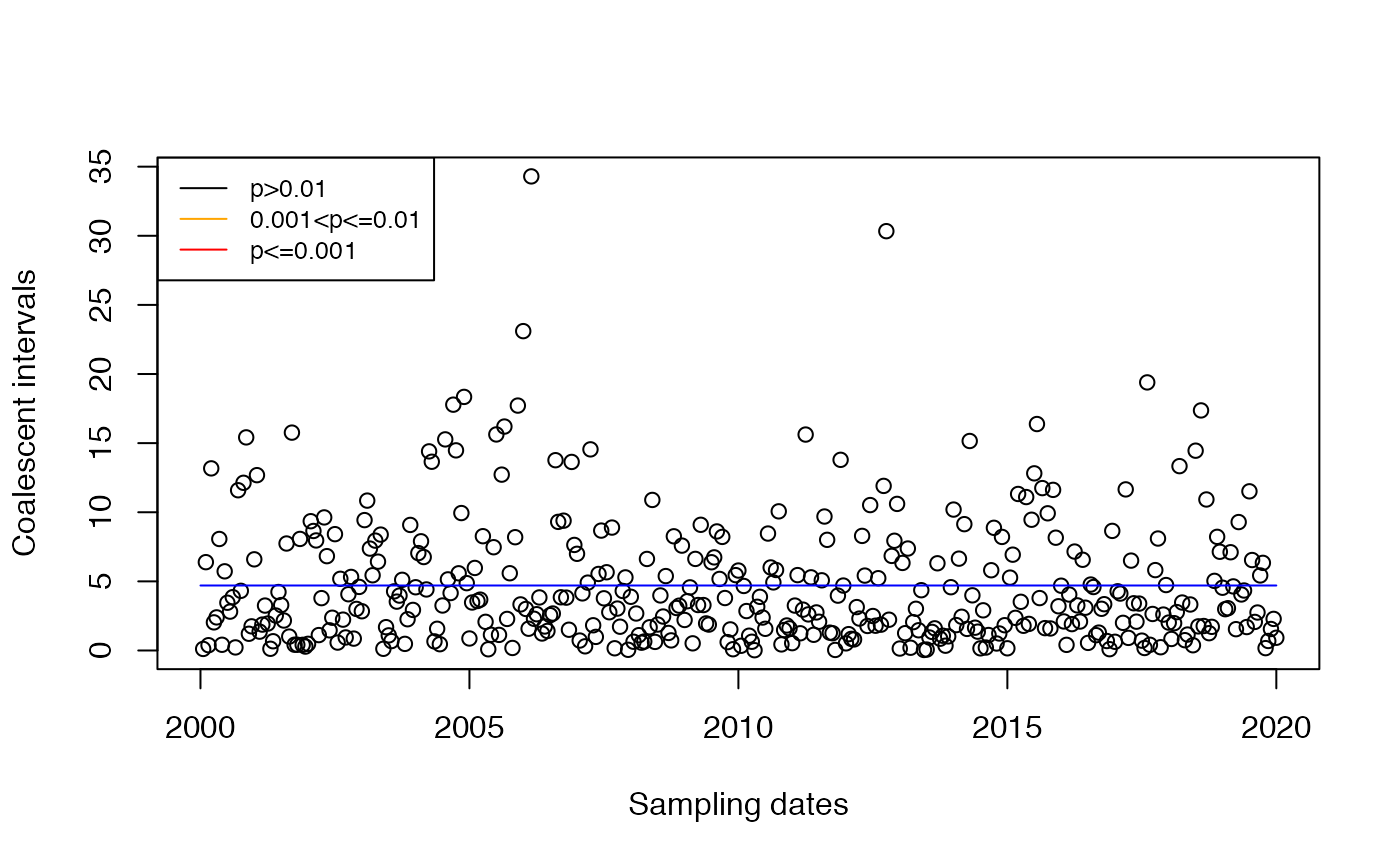
Simulation with varying population size
Now we consider that the effective population size is not constant but is a continuous function \(N_e(t)\) of time.
set.seed(0)
Ne=function(t){if (t>2010|t<2005) return(2) else return(10)}
tree=simCoal(seq(2000,2020,0.05),Ne)
plotBoth(tree,Ne)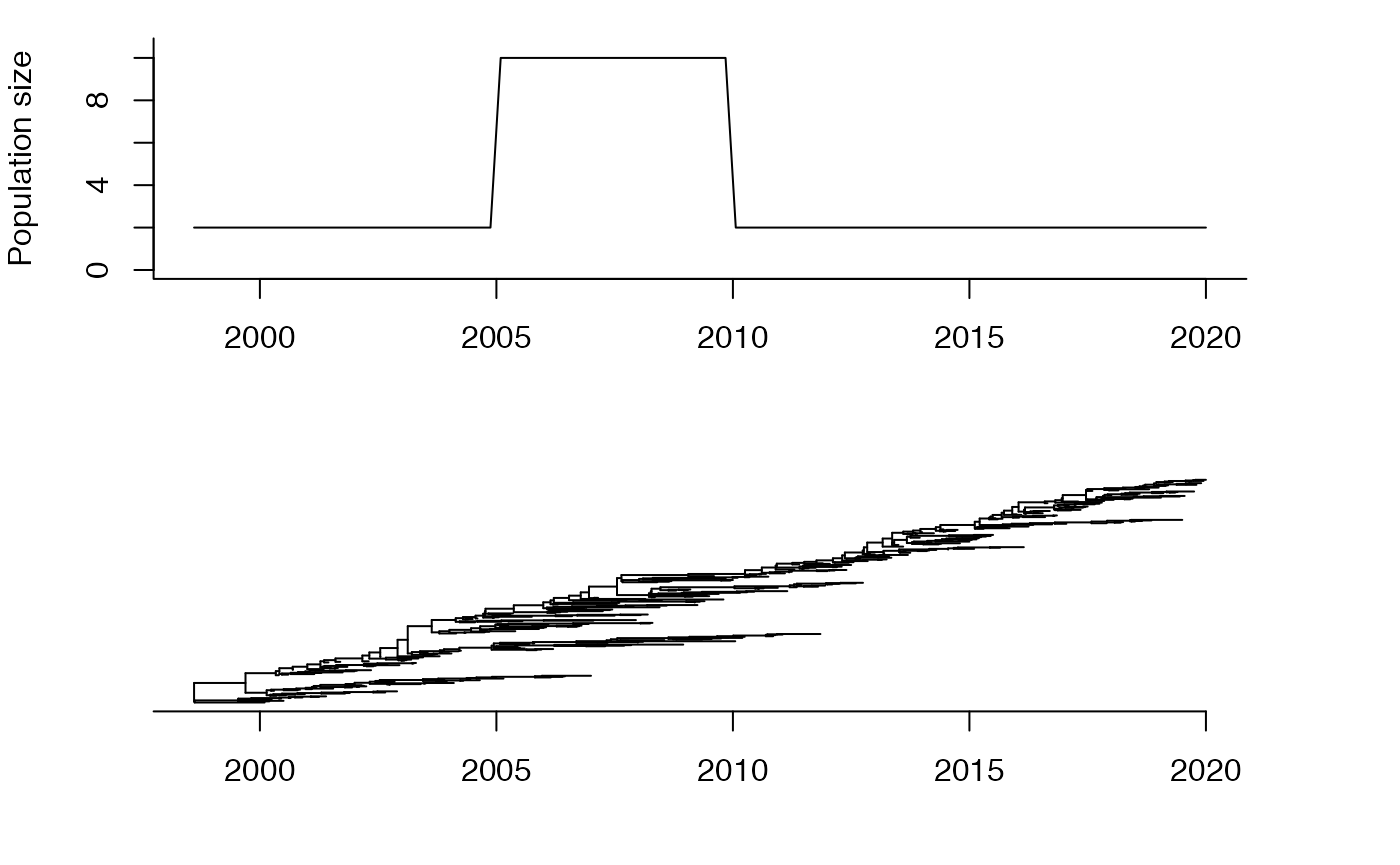
Coalescent intervals
The coalescent intervals \(C_k\) are no longer exponential and no longer iid as in the case of a constant population size. But we can still compute them and plot them as before:
plotCoalInt(tree)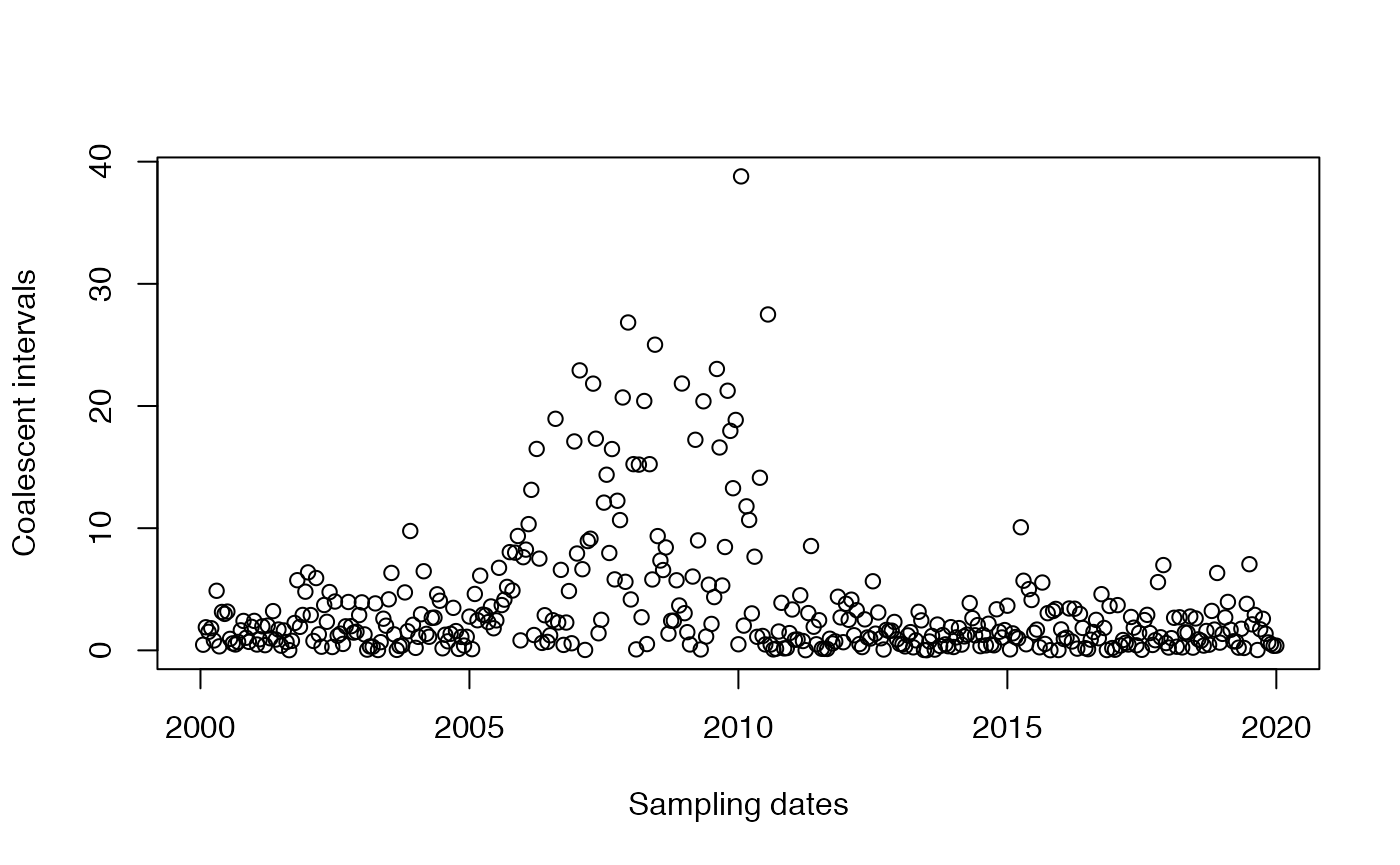
Bad test
If we apply the same test as before, we will get some false positives in the detection of imports:
res=detectImportsFAST(tree,constant=T)
plot(res)
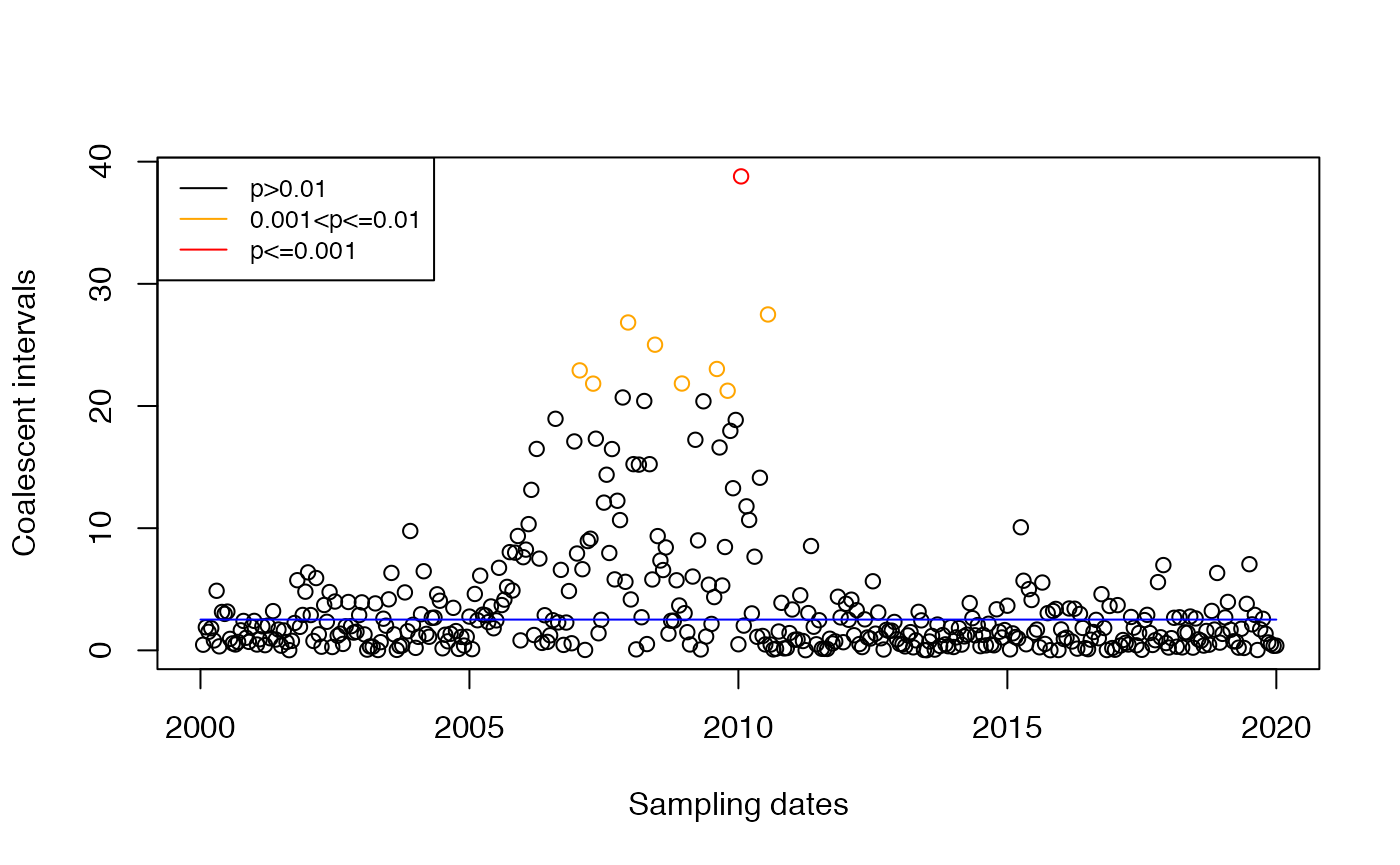
Detection of imports
Outliers in the distribution of \(C_k\) against \(s_k\) are likely imports. The distribution \(p(C_k|s_k)\) is unknown and complex in the general case. We use a test in which the distribution is assumed exponential with time-changing mean \(\hat N_e(t)\) estimated. This is not quite correct since the distribution is not exponential, but matching the mean is a good first step. As a first attempt, let’s consider the estimator based on the median of other coalescent intervals around the same time: \[\hat N_e(s_k)=\frac{\mathrm{median}(C_{j\neq k\mathrm{~with~}|s_k-s_j|<\epsilon})}{\mathrm{ln}(2)}\]
This estimator is used in the fast test of DetectImports:
res=detectImportsFAST(tree,constant=F,epsilon=1)
plot(res)
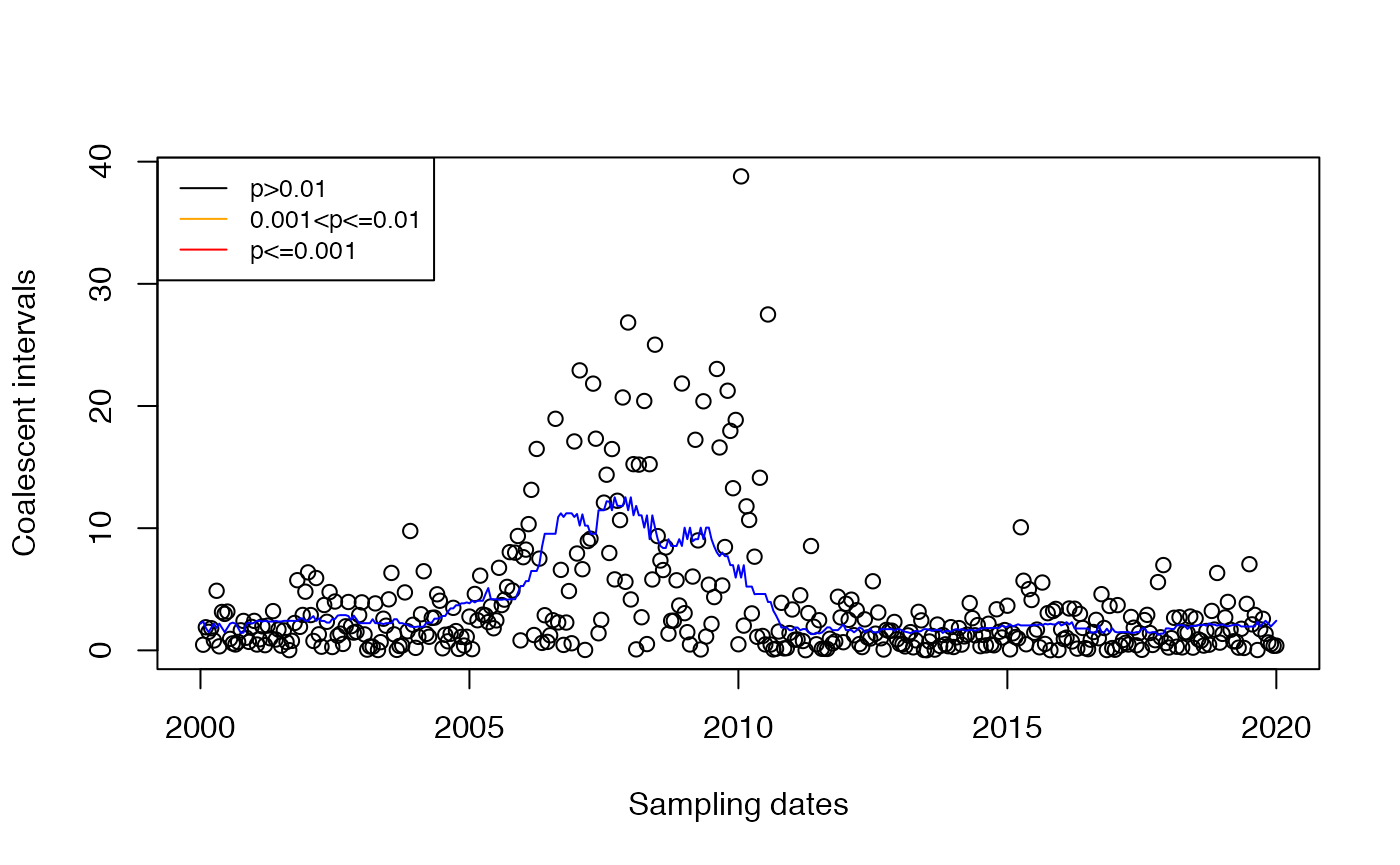
We can see that the false positives are no longer present. In the DetectImports paper, we develop a test based on the same principle but using Bayesian statistics.